OCB is a block-cipher mode of operation. It simultaneously provides both privacy and authenticity. A scheme which accomplishes both of these goals is called an authenticated-encryption scheme. OCB was designed largely in response to NIST's modes-of-operation activities. It is follow-on work to Charanjit Jutla's IAPM.
In the past, when one wanted both privacy and authenticity, the usual thing to do was to separately encrypt and compute a MAC. (MAC stands for message authentication code.) The encryption is what buys you privacy and the MAC is what gets you authenticity. One needs to be a little bit careful to properly combine an encryption scheme and a MAC (here's a recent paper on the generic composition approach; also see the What are the alternatives to OCB? question). Still, the approach, done right, is clean and correct. But the cost to get privacy+authenticity in this way is about the cost to encrypt plus the cost to MAC. If one is encrypting and MACing in a conventional way, like CBC encryption + the CBC MAC, the cost for privacy+authenticity is about twice the cost for privacy alone. Thus people have often hoped for a simple and cheap way to get message authenticity as an incidental adjunct to message privacy. Usually they have failed quite miserably.
What makes OCB
interesting is that it
provably achieves both privacy and authenticity,
and it accomplishes this in way that is almost as cheap
as getting privacy alone.
Has any paper on OCB appeared?
Yes, the OCB paper appeared at
the Eighth ACM Conference on Computer and Communications Security (CCS-8).
Is the notion of authenticated encryption something new?
Yes and no.
The general idea to combine
privacy+authenticity is folklore, and lots of attempts can
be found in the security literature and in systems.
Nobody was solving this problem correctly, but nobody in the
cryptographic community was paying any attention.
Bellare and I finally presented
definitions for the goal (based on an old manuscript of ours)
in an Asiacrypt 2000 paper, and
the same definitions appeared, independently, in a
Eurocrypt 2000 paper by Katz and Yung.
So I site these two papers for the origin of the
definition of the goal.
I also reference an Asiacrypt 2000 paper by
Bellare and Namprempre, which looks at the notion
in much greater depth.
It's a pretty common story that a folklore cryptographic goal fails
to get a proper cryptographic treatment for a long, long time.
I suppose there aren't many trained, "modern", cryptographers,
and a good fraction of us focus our interests on issues that are
not closely related to actual cryptographic practice.
Is it safe to combine privacy and authenticity?
Some people think that it's
"dangerous" to try to combine privacy and authenticity. They
believe that
you won't get the expected degree of authenticity from the combined
privacy/authenticity transformation.
This belief springs from the history of wrong attempts in trying to
add in authenticity to encryption schemes.
It also comes from the realization that many
people (including some well-known security folks) used to
believe, wrongly, that standard ways to get privacy, maybe
with "redundancy" thrown in, already implied authenticity.
Anyway, these past errors have nothing to do OCB.
There, privacy and authenticity are correctly combined. This is proven.
There's no danger involved when you correctly combine privacy and
authenticity.
But there's a big danger if you try to do this at home.
This is a very tricky problem,
and a home-grown solution will invariably be wrong.
What does the name stand for?
It stands for offset codebook. That's a (highly abbreviated)
operational
description of what is going on in the mode
(where, for most message blocks,
one offsets the block, applies the block cipher, and then offsets the
result once again).
If I had named the algorithm by a
functional description instead of an operational
one it might have been called AEM,
for Authenticated-Encryption Mode.
But I think I'll stick with OCB.
What block cipher should I use with OCB?
You can use OCB with any block cipher that you like.
But the obvious choice is AES.
AES actually comes in three flavors: AES128, AES192, and AES256. The choice is yours. But I like AES128. (You know, NIST would have me write "AES-128" instead of "AES128". But I don't like that dash.)
If you use OCB with a block cipher having a 64-bit block length
instead of a 128-bit block length, beware
that you'll get a worse security bound. You'll need to change keys
well before you encrypt 2^32 blocks (as with all well-known
modes that use a 64-bit block cipher).
In any case, it seems strange to combine a modern mode like OCB
with an old block cipher like DES. Choose a modern,
128-bit block cipher. Like AES or RC6.
Should one write "OCB-AES" or "AES-OCB"?
Personally, I prefer to go from high-level protocol on down:
OCB-AES (or OCB-AES128), just like HMAC-SHA1.
On the other hand, the block cipher has always been what
people like to focus on, and, in English, adjectives do precede nouns.
So I sympathize with the contrary ordering.
In the paper I write OCB[E,t] (where E is the block cipher and
t is the tag length).
Who invented OCB?
I did (Phil Rogaway). But I had help from Mihir Bellare, John Black , and Ted Krovetz. Among other contributions, they helped to shoot down my earlier, buggy attempts.
Who am I? I'm an Associate Professor in the
Department of Computer Science
at the
University of California, Davis.
I also have an appointment in the
Department of Computer Science,
Faculty of Science, at
Chiang Mai University.
My area of research is (you guessed it!) cryptography.
For the last 10+ years I've helped develop a
style of cryptography I call "practice-oriented provable security."
This framework is a perfect fit
to the problem of designing an authenticated-encryption scheme.
In general,
one of the "outputs" of practice-oriented provable security
has been cryptographic schemes which are highly appropriate for standards.
Though never before being directly
involved in any standardization effort,
some of my work has managed to find its way into cryptographic
standards due to the good work of others.
In particular, I am co-inventor on the schemes
known as OAEP, DHIES, and PSS/PSS-R, which
are in standards or draft standards of
ANSI, IEEE, ISO, PKCS, SEC, and SET.
Is OCB in any standards?
OCB is in a draft standard of IEEE 802.11.
This is a standard for Wireless LANs.
And OCB is a submission to NIST, for consideration as a
new mode of operation. NIST might elect to
standardize OCB, or they might base a standard on some
other authenticated-encryption mode,
or they might elect not standard any
authenticated-encryption mode at all.
I expect that
it depends, in part, on what sort of public feedback they receive.
OCB isn't yet in any approved standard; it is too young for this
to have happened already.
But I expect that OCB will, eventually, be widely standardized.
I'm not the first to give a (cheap and correct) authenticated-encryption mode of operation. That honor falls on Charanjit Jutla, from IBM Research. Jutla was the first to publicly describe a correct block-cipher mode of operation that combines privacy and authenticity at a small increment to the cost of providing privacy alone. Jutla's scheme appears as IACR-2000/39.
Jutla actually described two schemes: one is CBC-like (IACBC) and one is ECB-like (IAPM). The latter was what we built on. In fact, OCB maintains high-level ideas from Jutla's scheme, but adds several more tricks. One might consider OCB as IAPM after an exhausting amount of "crypto-engineering".
Whenever you reference OCB, please be sure to reference
Jutla's work, too.
There's an unfortunate tendency in computer science to reference the last
work in some sequence of work, sometimes losing other key
points along the chain.
Jutla's paper appears as
"Encryption modes with almost free message integrity",
Advances in Cryptology - EUROCRYPT 2001,
Lecture Notes in Computer Science, vol. 2045,
B. Pfitzmann, ed., Springer-Verlag, 2001.
What did Gligor-Donescu do?
Virgil Gligor and Pompiliu Donescu
have also described an authenticated-encryption
mode, XCBC, in
[Gligor, Donescu; 18 August 2000]
(Postscript or
pdf, from
Gligor's homepage ).
The mode is not similar to OCB, but
it is similar to Jutla's IACBC.
We do not know the history of
Gligor and Jutla in devising their schemes, but
Jutla's scheme was publicly distributed before Gligor's.
OCB was invented after both pieces of work made their debut.
Academically, from my reading, the main new contribution of [Gligor, Donescu] is the suggested use of mod-2^n arithmetic in this context. In particular, [Jutla] had suggested the use of mod-p addition, and it was non-obvious that moving into this weaker algebraic structure would be OK.
Later versions of [Gligor, Donescu; 18 August 2000] have added in new schemes. Following Jutla, [Gligor, Donescu; October 2000] mention a parallelizable mode of operation similar to Jutla's IAPM. Following my own work, [Gligor, Donescu; April 2001] have updated all of their modes to use a single key and to deal with messages of arbitrary bit length.
Gligor indicates that he has filed patent applications on
his ideas, and he also indicates that these were
filed at an earlier date than what IBM indicates for its
patent filing.
The contents of all of these patent filings are confidential,
and I have no idea what is in any of them.
All I know is that I am unaware of any idea from
Gligor's academic paper which OCB makes use of.
To me, OCB is follow-on work to Jutla's IAPM, but is
not derivative of any ideas communicated in [Gligor, Donescu; 18 August 2000].
What is a nonce and why do you need one?
In OCB, you must present a 128-bit nonce each time you want to encrypt a string. (Assume we're using a 128-bit block cipher.) When you decrypt, you need to present the same nonce. The nonce doesn't have to be random or secret or unpredictable. But it does have to be something new. In general, a nonce is a string that is used used at most one time (either for sure, or almost for sure) within some established context. In OCB, this "context" is the "session" associated to the underlying encryption key K. For example, you may distribute the key K by a session-key distribution protocol, and then start using it. The nonces should now be unique within that session. Generating new nonces is the user's responsibility, as is communicating them to the party that will decrypt. A counter makes a perfectly good nonce, as does a random value.
A nonce is nothing new or strange for an encryption mode. All encryption modes which achieve a "strong" notion of privacy need to have one. If there were no nonce there would be only one ciphertext for each plaintext and key, and this means that the scheme would necessarily leak information (e.g., is the plaintext for the message just received the same as the plaintext for the previous message received?). In CBC mode the nonce is called an IV (initialization vector) and it needs to be adversarially unpredictable if you're going to meet a strong definition of security. In OCB we have a lower requirement on the nonce, and so we refrain from calling the nonce an IV. But you are welcome to call the nonce an IV, if you prefer!
What happens if you repeat the nonce? You're going to mess up authenticity for all future messages, and you're going to mess up privacy for the messages that use the repeated nonce. So don't do this. It is the user's obligation to ensure that nonces don't repeat within a session.
We note that all of the modes fail to meet the
customary notions of security if you repeat their IV/nonce.
There doesn't seem to be any known and formalized basis for speaking
of some modes failing "worse" than others when this happens.
What are some of OCB's properties?
OCB has been designed to simultaneously have lots of desirable properties.
These include the following.
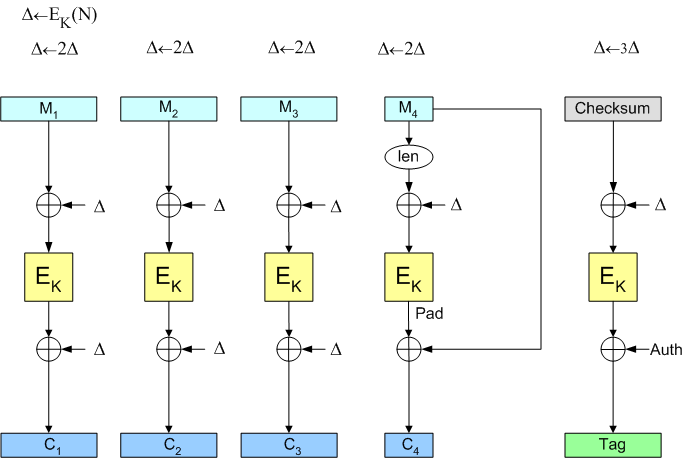
Let M be the message you want to encrypt-with-authenticity, and let K be the OCB encryption key, which is just an AES key. Let Nonce be the 128-bit nonce we will use. Let L be AES(K, 0). Define L(0) be L and, for i>0, let L(i) be L(i-1)<<1 if the first bit of L(i-1) is 0, and let L(i) be (L(i-1)<<1) xor 0x00000000000000000000000000000087 otherwise. Let L(-1) be L>>1 if the last bit of L is 0, and let L(-1) be L>>1 xor 0x80000000000000000000000000000043 otherwise. Break the message M into blocks M[1]M[2]...M[m] where each block except the last one has 128 bits. The last one may have fewer than 128 bits (but it has 0 bits only if the message M is empty). Now we encrypt as follows.
function ocb-aes-encrypt(K, M, Nonce)
begin
Offset = AES(K, Nonce xor L)
Checksum = 0
for i = 1 to m-1 do begin
Offset = Offset xor L(ntz(i))
Checksum = Checksum xor M[i]
C[i] = Offset xor AES(K, M[i] xor Offset)
end
Offset = Offset xor L(ntz(m))
Pad = AES (K, len(M[m]) xor L(-1) xor Offset)
C[m] = M[m] xor (the first |M[m]| bits of Pad)
Checksum = Checksum xor Pad xor C[m]0*
FullTag = AES(K, Checksum xor Offset)
Tag = a prefix of FullTag (of the desired length)
return C[1]... C[m-1] C[m] Tag
end
To decrypt, do the reverse process, making sure that the presented Tag is as expected (if not, regard the presented ciphertext as invalid).
Here is a different representation of OCB, now as a picture. The picture should be read from left-to-right: first we compute the Offset, then we use this Offset on each message block, updating the Offset each time. As above, the Checksum is the xor of the first m-1 message blocks xor the Pad xor the padded C[m] value.

Is there code available? Is it free?
Yes there's code and yes it's free.
The code is here.
First, there's a reference version in C. It's not particularly fast, but it should help clarify the algorithm if you only think in code. It was written by Ted Krovetz, with some help from John Black and me. Paulo Barreto wrote an implementation in Java. Thanks, Paulo! Ted and I have been working on an optimized version in C. We work on this during our copious free time. We'll release that code as soon as it is ready (maybe late June?). There's also a Pentium assembly version that Ted wrote so that I'd have assembly timing figures to report. Ted hasn't released this code. If you yourself write an OCB implementation that you're proud of, please send it to me and I'll happily drop it to the web page.
In correctly coding OCB, I think the biggest difficulty is
endian nonsense. The spec is subtly big-endian
in character, a consequence of it's use of "standard"
mathematical conventions.
If your implementation doesn't agree with mine,
chances are high that there's some stupid endian error that will
take you way too many hours to find and understand.
Are OCB test vectors available?
Yes, for OCB-AES128, OCB-AES192, and OCB-AES256.
They're all here.
In the past, it was wise to wait for a few years before using any new cryptographic scheme. One needed to give cryptanalysts a fair chance to attack the thing. Assurance in a scheme's correctness sprang from the absence of damaging attacks by smart people, so you needed to wait long enough that at least a few smart people would try, and fail, to find a damaging attack. But this entire approach has become largely outmoded, for schemes that are not true primitives, by the advent of provable security. With a provably secure scheme, assurance does not stem from a failure to find attacks; instead, assurance comes from proofs (with their associated bounds and definitions). Our work includes a proof that OCB-E is secure as long as block cipher E is secure (where E is an arbitrary block cipher and "secure" for OCB-E and secure for E are well-defined notions).
Of course it is conceivable that OCB-AES could fail because AES
could have a major problem.
Or a definition or proof could have a major bug.
Or there could be some other, completely unforeseen issue;
in cryptography, practical guarantees are never absolute.
But all of these possibilities seem very remote, in this case.
With OCB we are in a domain
where the underlying definition is simple and rock solid,
where timing attacks are not a big concern,
where there are no "random oracles" to worry about,
and
where the underlying cryptographic assumptions are completely standard.
As for the possibility of AES itself having a major problem, I believe that
all of the AES finalists are safe, conservative, algorithms, representative
of state-of-the-art practice. I think it is safe to use any of them.
No doubt there will be progress in the cryptanalysis of AES,
but it would be pretty shocking if a practical attack emerged.
What is the generic-composition alternative to OCB?
If you need privacy+authenticity but don't want to use OCB,
for whatever reason, I suggest you go with
the
generic composition approach.
This approach has been around forever, and it is versatile and clean.
Using separated keys, you should encrypt the plaintext and then MAC the
resulting ciphertext. You can use any encryption scheme and any MAC
that you like, and the composite scheme is guaranteed to do what it should do.
I view the generic composition approach as the main "competition" to OCB,
so I want to make sure that people understand what this alternative is.
To offer the same basic "service" as OCB (correctly dealing with arbitrary-length plaintexts, getting a "minimal-length" ciphertext, and using an arbitrary nonce), you'll need, in the end, to do something like this. For privacy, use CBC mode with ciphertext-stealing and an IV derived by enciphering the nonce. For authenticity, use the CBC MAC variant known as "XCBC" suggested by Black and Rogaway (dvi or PostScript or pdf). Use standard key separation to make all the needed keys.
Spelling it all out (since no standard I know has done so), suppose you want to encrypt+authenticate an arbitrary message M using a 128-bit key K and AES128. Then first derive 128-bit subkeys K0=AES(K,0), K1=AES(K,1), K2=AES(K,2), and K3=AES(K,3). Break the message M into M[1]M[2]...M[m], where each block M[i] except the last one has 128 bits. The last one may have fewer than 128 bits, but it will have 0 bits if and only if the message M is empty. Let Nonce be a 128-bit nonce (provided by the party that encrypts); let C[0]=AES(K0,Nonce); for i=1 to m-1 let C[i] = AES(K0,C[i-1] xor M[i]); let C[m]=M[m] xor the-first-|M[m]|-bits-of-AES(K0,C[i-1]); let C'=Nonce.C[1].....C[m]; let FullTag be the CBC MAC (Black-Rogaway variant) of C' under a key of K1.K2.K3; and let Tag be a desired-length prefix of FullTag. The ciphertext for plaintext M is C=C[1].C[2].....C[m].Tag, which must be communicated along with the nonce Nonce.
Compared to OCB, the above instantiation of the generic composition approach is slower and not parallelizable. And, when all is said and done, perhaps it is disappointingly complex. But a method like the one just given provides privacy+authenticity, has good assurance, and it should keep you clear of any patents.
If you want a parallelizable scheme from the generic composition approach, I suggest to combine CTR-mode encryption and PMAC. Do key separation to make the encryption key and the MAC key; encrypt the message with CTR-mode; then MAC the ciphertext, including the CTR, with PMAC.
In combining privacy and authenticity yourself, be careful
to avoid the following pitfalls:
(1) a failure to properly perform key separation;
(2) a failure to use
a MAC which is secure across different message lengths;
(3) omitting the Nonce from what is MACed;
(4) encrypting the MACed plaintext as opposed to the superior method
(at least with respect go general assumptions)
of MACing the computed ciphertext.
What are the advantages of OCB compared to generic-composition?
OCB is a single algorithm that
offers up the security service that most applications require.
This makes OCB less likely to be misused.
(It is all too common
that encryption and authenticity mechanisms get misused:
authenticity is
assumed but now provided; IVs are defined wrong; length-variability is
messed up; keys are not separated; and so on.)
Compared to generic composition, OCB will, typically, be about twice as fast. It will also use less key material. In a low-power environment, it will probably use less power. OCB has been designed to give minimal-length ciphertexts and to work correctly on messages of arbitrary length. Generic composition can deliver these last properties, if done right, but usually it is not. Because OCB is parallelizable, it can be made to run faster and faster as machines offer up more and more exploitable parallelism. Whether or not generic composition gives a parallelizable scheme depends on what is being combined. But typically one would be combining non-parallelizable schemes and so the result is not parallelizable.
One colleague whom I respect
feels that it is, overall, a disadvantage to combine
privacy and authenticity; he
thinks it is "architecturally wrong".
I maintain that even if one felt on aesthetic
grounds that privacy and authenticity should be kept separate,
still:
(1) performance matters a lot; and
(2) it is better that
privacy is understood to mean
indistinguishability under chosen-ciphertext attack,
and I know of no better way to get this type of "strong privacy" than OCB.
I have also heard the complaint that a combined scheme doesn't
allow for weak-privacy combined with strong-authenticity.
I would answer that I don't know why anyone
(outside of certain spy agencies!)
would want this combination;
better to have
strong privacy combined with strong authenticity.
Please compare OCB to Jutla's and Gligor-Donescu's schemes
Jutla has proposed two modes, IACBC and IAPM (but it now looks as
though Jutla is backing off of IACBC and going with IAPM).
The latter is the parallelizable scheme, and therefore the one to
compare to OCB.
Two different methods are specified for offset generation in IAPM.
The simpler one (and what the author now appears to favor)
is based on mod-p addition, where p is the largest
prime less than 2^128.
Each offset is obtained from the previous one by a mod-p addition.
(Actually, the latest version of Jutla's work uses what I call
"lazy mod-p addition", a suggestion I had made in the
October version of the OCB algorithm definition).
On the plus side, the offset generation
is conceptually simpler than
the offset generation used in OCB; it will
require less control logic in hardware;
it will need fewer lines of code in software.
On the downside,
this mod-p addition (instead of xor) will substantially increase
overhead, in some environments;
it makes the scheme endian-biased; and
the need for a 128-bit addition circuit
may, in hardware, increase chip area.
Based on these same tradeoffs, OCB abandoned
the use of lazy mod-p addition for the final spec.
Jutla also gives an entirely xor-based scheme, but it is not competitive with OCB in terms of key-setup cost. Key setup will be several times the cost of key-setup in OCB, depending, mostly, on the maximal length plaintext that may be encrypted. Alternatively, key-setup costs are not increased, but control flows is made substantially more complex and there is an additional logarithmic overhead per message. That overhead is particularly unpleasant on short messages.
No padding regime is specified in IAPM, so IAPM does not, at present, apply to arbitrary bit strings. Once a padding regime is added, say obligatory 10*-padding, the length of ciphertexts will be longer than OCB ciphertexts any time that the message being encrypted is a non-multiple of 16 bytes. The increase in length will range from 0 to 127 bits (ie., up to 16 extra bytes). IAPM uses twice the key material of OCB (two AES keys instead of one).
The most recent version of [Gligor, Donescu] now contains four authenticated encryption schemes, which the authors call XCBC$-XOR, XCBC-XOR, XCBCS-XOR, and XECBS-XOR. Only the last of these modes (see Section 4 of the authors' addendum) is parallelizable. The addition of a parallelizable scheme to [Gligor, Donescu] has come subsequent to the publication of Jutla's work; what is more, XECBS-XOR is similar to Jutla's IAPM (though no credit is given). XECBS-XOR uses mod 2^n addition instead of mod-p addition. This difference might suggest an efficiency improvement, since a comparison and possible addition is saved. But I am doubtful: per block of plaintext, [Jutla] uses one mod-p addition and three 128-bit xors; [Gligor, Donescu] uses three 128-bit additions and one 128-bit xor. One should think of xors as significantly cheaper than both mod-p addition and 128-bit addition, so it seems unlikely that there has been any net gain. The use of additions again makes the scheme endian-biased. One expects the use of an additive ring (integers mod 2^n) instead of a field (GF(p) or GF(2^n)) to worsen any possible security bound by at least a log factor. But, in any case, no proof has been suggested for this mode, and earlier proofs for another mode were not verifiable (at least by me). Following my own work, the [Gligor, Donescu] modes include the use of techniques so as to use a single key and to deal with messages of arbitrary bit length. However, the techniques are not pushed as far as with OCB, and so there is ciphertext-expansion (up to 16 bytes) for all messages which are a non-multiple of 16 bytes.
Basically,
I started off knowing Jutla's and Gligor-Donescu's August manuscripts,
and then spent hundreds of hours to try to create the most
efficient and elegant algorithm and writeup that I could,
given this starting point. Just one algorithm;
I viewed it as my responsibility to make whatever design
choices were needed to arrive at one solution.
Having spent a decade of my life developing a line
of research which seemed "tailor made" for this particular project,
it seemed that nobody else would be in a better position to choose
among competing algorithmic possibilities and push through a proof.
The proof was co-developed along with the algorithm, and
difficulties encountered in the proof would
often point to actual problems in the algorithm.
More than fifteen version of OCB were studied before
arriving at the final definition.
Many of the design choices are explained in the paper.
Does Phil have a patent on OCB?
Yes, I did file patent applications covering the new techniques
used in OCB.
There was a filing on 12 October 2000, and a filing on
9 February 2001.
If you want to use OCB in a commercial product,
you'll need to get a license from me.
But I'll license this IP under
fair, reasonable, and non-discriminatory terms.
All companies will be offered the same license agreement.
I expect licensees to pay a modest, one-time fee.
Here is a patent-assurance letter
I wrote for the IEEE, which mandates
OCB in a draft 802.11 (Wireless LAN) standard, as part of the
WEP ("Wired Equivalent Privacy") protocol.
How much will a license cost?
Not much.
I intend that no solvent company should
find licensing from me to be a significant issue in their
cost of doing business.
Here is an offer letter indicating
how I am licensing OCB.
Has OCB already been licensed?
Yes, it has. But, unfortunately, I am not at liberty to say more.
Will anyone else come to have a valid patent that covers OCB?
Unfortunately, this question is impossible to answer at this point.
IBM has indicated that it has a patent filing that covers
Jutla's authenticated-encryption work.
They indicate that this was filed on 14 April 2000.
Gligor has indicated that he has three patent filings that cover his
authenticated-encryption and parallelizable MAC work.
He indicates that these were filed on 31 January 2000,
31 March 2000, and 24 August 2000.
All of these filings were provisional patent filings.
One can only conjecture who will have what enforceable rights. As for Jutla/IBM, I have been clear all along that OCB retains similarities to Jutla's IAPM. Intellectually, OCB owes much to Jutla's work. But whether or not IBM's patent covers OCB may depend on how broadly IBM's claims were crafted.
As for Gligor/VDG, I am unaware of any idea from [Gligor, Donescu; 18 August 2000] that I used in OCB. I believe that any utility patent filed after Jutla's work and my work appeared but based on a provisional patent filed before Jutla's work and my work appeared will need to be examined with care, comparing the contents of the utility patent to the contents of the provisional patent, and paying attention to what was published in the interval. Such an exercise is currently impossible, because provisional patents are not made available before utility patents issue.
I start to think that I have been too
talkative and too concerned about what IP other
parties could come to hold. In truth, nobody ever
knows the answer to this question.
How can one authenticate cleartext data when using OCB?
It is common to want to authenticate unencrypted data, such as a packet header, when carrying out authenticated encryption. We call this string of unencrypted data the associated data. The associated data should be bound to the ciphertext in such a way that if the adversary tries to change it, this will, almost certainly, be detected by the Receiver.
If we were using the generic composition paradigm, say with the recommended encrypt-then-MAC method, handling associated data would be easy: the associated data is put in the scope of the MAC but it is never encrypted. When using a mode like OCB, however, it is not clear what to do. The initial design of OCB did not directly provide for associated data. Many people quickly demanded this feature and so OCB was extended, many months ago, to allow for associated data. Here are mechanisms that I support.
First, one can hijack a portion of OCB's n-bit nonce and drop some or all the associated data there. For example, when using AES and a nonce which is a 32-bit counter there are 96 unused bits of the nonce field. These may be used to hold associated data.
When the associated data does no fit into unused bits of the nonce field (or when the application simply does not want to use those bits for that purpose), do the following: given a key K, associated data H, a message M, and a nonce Nonce, compute Δ = PMAC(K, H) and compute C || Tag = OCB(K, M, Nonce) and return C || (Tag xor Δ). An exception is made to the value of Δ when H is the empty string; in that case, let Δ be the string of t zero-bits.
The above solution is particularly simple when |H| is less than the blocksize n of the underlying block cipher E; in that case Δ = PMAC(K, H) = E(K, H 10*) where H 10* means H with appended 10…0-padding.
Among the pleasant features of this OCB extension are the following: (1) it avoids wasting block-cipher calls; (2) it allows H to have arbitrary length; (3) it avoids using additional key material or additional key separation; (4) it retains the parallelizability of OCB; (5) when H is constant over the course of a session Δ can be pre-computed, saving time; (6) it upwardly extends OCB; and (7) it rests on a worked-out theory, supported by provable-security definitions and proofs.
It is important to understand that an authenticated-encryption scheme that allows associated data is not the same, definitionally, as an authenticated-encryption scheme which does not. New definitions and proofs must be fashioned to deal with this novel kind of object. I have done this, but the definitions and proofs in support of this OCB extension have yet to be published as a refereed paper. (A paper on this topic has been submitted.) A preliminary paper, giving the construction we have stated, does appear on NIST's modes web site, while the full paper will be distributed soon.
We comment that this OCB extension
was suggested many months ago and has
been completely "stable"; we see no problem using it right away.
There are no added IP issues; any
license covering OCB will of course cover this
extension.
What if Phil vanishes?
If I get eaten by a python
or am done in by a mad tuk tuk driver,
you can
contact my backup, Michael Biesanz, at michaelb@hevanet.com.
Where can I learn more
Why, read the paper, of course!