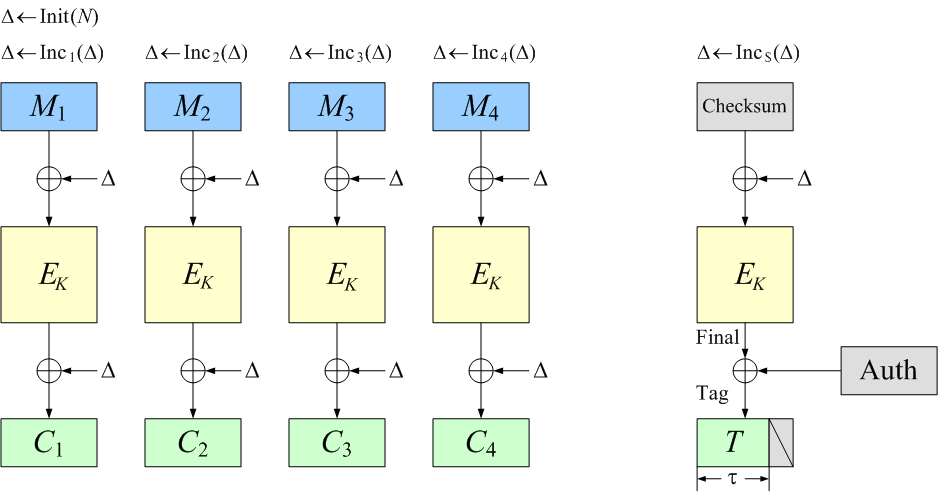
OCB is a blockcipher-based mode of operation that
simultaneously provides
both privacy and authenticity for a user-supplied plaintext.
Such a method is called an authenticated-encryption scheme.
What makes OCB remarkable
is that it achieves authenticated encryption in almost the same
amount of time as the fastest conventional mode, CTR mode, achieves privacy alone.
Using OCB one buys privacy and authenticity about as cheaply (or more cheaply—CBC was once the norm) as
one used to pay for achieving privacy alone.
Despite this, OCB is simple and clean,
and easy to implement in either hardware or software.
OCB accomplishes its work without
bringing in the machinery of universal hashing,
a technique that does not seem to lend itself to implementations
that are simple and fast in both hardware and software.
In the past, when one wanted a shared-key mechanism providing
both privacy and authenticity,
the usual thing to do was to
separately encrypt and compute a MAC, using two different keys.
(The word MAC stands for Message Authentication Code.)
The encryption is what buys you privacy and the
MAC is what gets you authenticity.
The cost to get privacy-and-authenticity in this way is
about the cost to encrypt (with a privacy-only scheme) plus the cost to MAC.
If one is encrypting and MACing in a conventional way,
like CTR-mode encryption and the CBC MAC,
the cost for privacy-and-authenticity is
going to be twice the cost for privacy alone, just counting blockcipher calls.
Thus people have often hoped for a simple and cheap way to get
message authenticity as an almost “incidental’ adjunct to message privacy.
Can you describe how OCB works?
Sure;
I’ll draw a pretty picture, too.
To make things concrete,
let’s assume you’re using a blockcipher of E=AES with 128-bit keys.
The block length is n=128 bits.
Let’s assume a nonce of 96 bits.
Other values can be accommodated,
but 96 bits (12 bytes) is the recommended nonce length.
 |
Are there different versions of OCB?
There are three named version of OCB, corresponding to three points in
time over the algorithm’s 10-year evolution.
If I need to be specific, I’ll say OCB1, OCB2, or OCB3.
I sometimes use the name “OCB” as a generic label for all of the different
versions. Other times I use OCB to mean the final algorithm, OCB3.
For example, when I described OCB in the section above, I was in fact describing OCB3.
I don’t like to change an algorithm I’ve published;
there should be a compelling reason to do so.
Let me describe what was significant with each algorithm in the chain.
- OCB1 — From the ACM CCS 2001 paper by Rogaway, Bellare, Black, and Krovetz.
- The scheme that my team first defined built on the ideas of Charanjit Jutla’s IAPM.
OCB1 brought to the table an ability to handle arbitrary-length plaintexts, doing so with
minimal expansion in the length of the ciphertext. To make this happen, message padding could not
be used. Also, IV requirements were minimized; the IV only had to be a nonce. The number
of blockciphers calls was reduced to m+2 for encrypting an m-block message.
We made do with a single underlying blockcipher key. The increment function was made simpler and
more efficient than what Jutla had described.
- OCB2 — From the Asiacrypt 2004 paper by Rogaway.
Buggy! Don’t use this.
- Mode OCB1 had a defect that practitioners were quick to point out:
it had not been designed to natively handle associated-data (AD).
Associated-data refers to stuff, say a message header, that
needs to be authenticated but should not encrypted.
Thanks to Burt Kaliski, of RSA,
for first bringing to my attention the need for AD support.
With OCB2 I added in support for AD.
I also implemented a new way of doing the increment (Inc) function, using
doubling instead of the table-based approach.
I had thought that doing increments by doubling would make for a faster scheme.
Finally, I recast things in the tweakable-blockcipher setting
that had been suggested earlier by Liskov, Rivest, and Wagner.
- OCB3 — From the FSE 2011 paper by Krovetz and Rogaway.
- The final version of OCB goes back to a table-based
approach for incrementing offsets (the Δ-values); experimental
findings made it clear that doubling was not the win that I had thought.
Beyond this, we (usually) shave off one blockcipher call and
(usually) eliminate the blockcipher latency that we used to suffer two or three times.
McGrew and Viega had complained about these two defects in a 2004 paper of theirs.
In doing this new work Krovetz and I wanted to demonstrate that the extra blockcipher
call and the extra bit of latency were
inessential aspects of the basic design.
We also wanted to see if these matters actually mattered.
We found that our changes did speed things up, although the improvement was
relatively small.
There were no security issues that motivated the evolution of OCB, although
a major bug in OCB2 was discovered by
Inoue, Iwata, Minematsu, and Poettering
(2020).
In refining OCB, I resisted the temptation to design
for “beyond birthday-bound”
security; while this can be done, the benefit, using currently known techniques, does not seem worth the
added complexity, assuming that one is using a 128-bit blockcipher.
The changes from OCB1 to OCB2 to OCB3 aren’t really all that big, so
why have I bothered to continue to refine this mode?
-
One answer is that I regard authenticated-encryption
as one of the crucial “outputs” of the cryptographic community; it is one a handful
of interfaces and abstractions where a cryptographer can create
something that may actually get used and make a difference. Given the primitive’s importance,
it seems to me that, in some sense,
my community has failed if we do not deliver,
and get into popular use, the best AE schemes that we can devise.
-
Beyond this, I got obsessed.
I wanted to achieve AE just as cleanly and efficiently as could be.
Even if a scheme was practical and record-setting fast,
it didn’t seem enough if it could be made faster or more elegant.
It was an accident—yet it seems a fitting fact—that OCB looks a lot like
OCD.
If you implement OCB, please use the final version, OCB3.
I hope the name OCB, when understood to be a particular algorithm,
is by now understood to mean OCB3.
What are some of OCB’s properties?
OCB has been designed to simultaneously have lots of desirable properties.
Listed in no particular order, these properties include the following.
- OCB uses an amortized m + a + 1.016 blockcipher calls, where
m is the blocklength of the plaintext M and a is the blocklength of the
associated data A.
This assumes a counter nonce. (In the worst case, when the nonce is not a counter, the
1.016 constant becomes the number 2.)
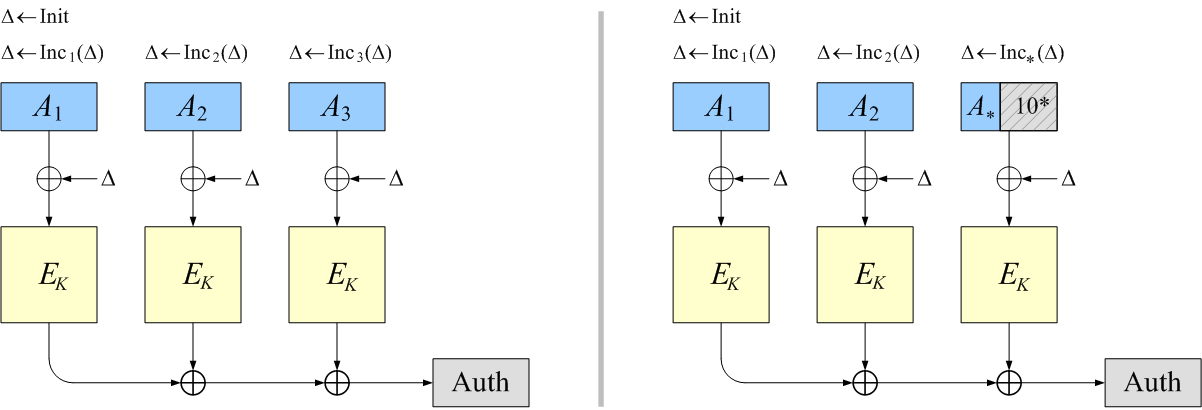
- If the header A is fixed during a session then, after preprocessing,
there is effectively no cost to have A authenticated: the mode
will use m + 1.016 blockcipher calls regardless of |A|.
- OCB is fully parallelizable: its blockcipher calls
may be performed simultaneously. (There is a dependency of the first block on the nonce-associated
blockcipher call one time in 64.)
Thus OCB is suitable for encrypting messages in hardware at
the highest network speeds, and it helps avoid pipeline stalls when implemented
in software. This is especially important in the presence of new AES instructions on
Intel processors. The parallelizability of OCB makes it suitable for use with bitsliced
AES implementations, too.
- Assuming the underlying blockcipher is not susceptible to timing attacks, natural implementations
of OCB would not be, either.
- OCB is on-line:
one need not know the length of A or M to proceed with encryption, and
one need not know the length of A or C to proceed with decryption.
- One can truncate the tag T to any number of bits and see the expected behavior.
For example, if one wants to use τ=32 bit tags, the adversary will
be able to forge each ciphertext with probability 1/232, but low query-complexity
or low computing-time attacks will not exist—in contrast, say,
to GCM (see the
Ferguson attack).
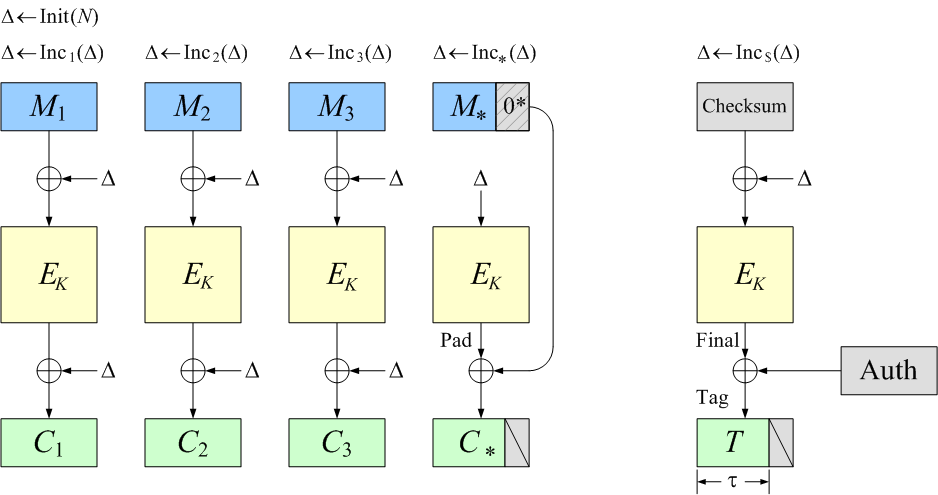
- OCB can encrypt messages of any bit length.
Messages don’t have to be a multiple of the blocklength, and no
separate padding regime is ever used.
No bits are wasted in the ciphertext due to padding;
ciphertexts are of “minimal” length.
- OCB allows arbitrary associated-data A to be specified when
one encrypts or decrypts a string.
This string will be authenticated but not encrypted.
- Encryption and decryption depend on a nonce N, which must be
selected as a new value for each encryption.
The nonce need not be random or secret.
A counter will work fine. Nonces may have any number of bits less than 128.
The recommendation is to use a 96-bit nonce.
- OCB uses a single key K for the underlying blockcipher, and all blockcipher
calls are keyed by K.
- The main computational work beyond the blockcipher calls consists of
three 128-bit xors per block.
- Key-setup would typically involve just a single blockcipher call and some doubling operations.
- OCB can be implemented to run in very little memory: the main memory cost is that needed to hold
the AES subkeys.
- OCB avoids 128-bit addition, which is endian-biased and can be expensive
in software or dedicated hardware.
In general, OCB is nearly endian-neutral.
- OCB respects word-alignment in the message and the header.
- OCB enjoys provable security.
One must assume that the underlying blockcipher is secure in the
customary (strong PRP) sense. Security falls off
in s2/2128
where s is the total number of blocks one acts on.
A very strong form of privacy is achieved:
nonce-based indistinguishability from random bits.
Likewise, a very strong form of authenticity is achieved:
nonce-based authenticity of ciphertexts.
- OCB nicely supports incremental interfaces. The processing of each
128-bit block of plaintext is independent of whether or not this is the final block of plaintext.
- The only parameters of OCB are the blockcipher E and the tag length τ. The message space
and nonce space are independent of these choices.
How much faster is OCB than CCM or GCM?
Usually much faster—like a factor of 2-6—but a precise answer
depends on a many factors. Please see the
performance page
for charts and tables across various platforms.
Is OCB good in hardware?
OCB was designed to perform well not only in software, but also in
hardware; the algorithm is efficiently realizable by
smart cards, FPGAs, and high-speed ASICs.
Pipeline delays have been minimized (especially in OCB3), and
short messages, like long ones, are optimized for.
Chip area, latency, and power consumption should be dominated
by the underlying blockcipher.
Here are a few papers that discuss hardware implementations of OCB:
What papers of mine deal with OCB?
OCB was developed over a sequence of academic papers published
between 2001 and 2011:
- The original OCB paper.
The proceedings version is in
ACM CCS 2001 and
the journal version is in
ACM TISSEC 2003.
- A paper about dealing with associated data. Appears in
ACM CCS 2002.
- A paper to develop the message authentication code, PMAC, that shaped the way AUTH
is computed in OCB. Appears in
Eurocrypt 2002.
- A paper about efficiently realizing tweakable blockciphers, and
about using tweakable blockcipher to improve OCB. Appears in
Asiacrypt 2004.
- A timing study about AE modes, along with refinements to get to the final
version of OCB. Appears at FSE 2011.
- Finally, an historical account on the design
and evolution of OCB. Appears in JoC 2021.
OCB is a well-known mode. It represents the
state-of-the-art for a blockcipher-based mode of operation for authenticated
encryption.
Is the notion of authenticated-encryption something new?
Yes and no.
The general idea to combine
privacy and authenticity is folklore, and lots of attempts can
be found in the security literature and in systems.
From a modern perspective,
the problem was routinely being solved incorrectly, but nobody in the
cryptographic community was paying much attention.
The first
definitions for the authenticated-encryption goal appeared in the
Asiacrypt 2000 paper BN00 of Bellare and Rogaway, and,
independently, in the
FSE 2000 paper KY00 of Katz and Yung.
Further investigation of the notion appears in the Asiacrypt 2000 paper
BN00 of Bellare and Namprempre.
Nonce-based notions of authenticated encryption were first formalized in the ACM CCS 2001 paper
cited above, while
the role of associated data was first formalized in the ACM CCS 2002 paper cited above.
What does the name stand for?
It was originally intended to stand for offset codebook.
That’s a highly abbreviated
operational description of what is going on in the mode:
for most message blocks,
one offsets the block, applies the blockcipher, and then offsets the
result once again.
I prefer you call the mode “OCB” than what this acronym was meant to suggest.
What blockcipher should I use with OCB?
You can use OCB with any blockcipher that you like.
But the obvious choice is AES.
AES actually comes in three flavors: AES128, AES192, and AES256.
I like AES128.
If you use OCB with a blockcipher having a 64-bit blocklength
instead of a 128-bit blocklength,
you’d get a worse security bound and would need to change keys
well before you encrypt 232 blocks (as with all well-known
modes that use a 64-bit blockcipher).
This is a fairly onerous requirement;
OCB is really only meant to be used with 128-bit blockciphers.
Should one write “OCB-AES” or “AES-OCB”?
I prefer OCB-AES (or OCB-AES128), going from high-level protocol on down.
Just like HMAC-SHA1.
Is OCB in standards?
OCB3 is defined in RFC 7253,
an informational RFC sponsored by the CFRG.
Before this, OCB1 was an optional method in the IEEE
802.11 standard,
where it was called WRAP (Wireless Robust Authentication Protocol).
Finally, OCB2 is specified in
ISO/IEC 19772:2009. That standard also includes AE
schemes CCM, GCM, EAX, and two further schemes.
Unfortunately, the
table of contents
seems to be all that I can legally provide for an ISO standard.
While OCB1 was submitted to NIST, it was never adopted as a NIST recommendation.
William Burr and others have explained that
NIST was reluctant to standardize any authenticated-encryption
mode with associated IP.
What did Jutla do?
I am not the first to give an integrated
authenticated-encryption mode of operation.
Charanjit Jutla, from IBM Research,
was the first to publicly describe a correct blockcipher-based mode
of operation that combines privacy and authenticity at a
small increment to the cost of providing privacy alone.
Jutla’s scheme appears as
IACR-2000/39.
He went on to publish the work in a
Eurocrypt 2001 paper.
A Journal of Cryptology
version appeared in 2008.
Jutla actually described two schemes: one is CBC-like (IACBC)
and one is ECB-like (IAPM). The latter
is what OCB builds on.
OCB uses high-level ideas from Jutla’s scheme
but adds in many additional tricks.
What did Gligor and Donescu do?
Virgil Gligor and Pompiliu Donescu
were working on authenticated-encryption schemes at the same time that Jutla was.
They described an authenticated-encryption mode, XCBC, in
[Gligor, Donescu; Aug 18, 2000], taken from
Gligor’s homepage.
The mode is not similar to OCB, but
it is similar to Jutla’s IACBC.
We do not know the precise history of
Gligor/Donescu and Jutla in devising their schemes;
Jutla’s scheme was publicly distributed first, but only by a little.
OCB was invented after both pieces of work made their debut.
One of the contributions of
[Gligor, Donescu] is the use
of mod-2n arithmetic in this context. In particular,
Jutla had suggested the use of
mod-p addition, and it was non-obvious that moving into
this weaker algebraic structure would be OK.
Later versions of [Gligor, Donescu; 18 August 2000] added in new schemes.
Following Jutla, [Gligor, Donescu; October 2000] mention
a parallelizable mode of operation similar to Jutla’s IAPM.
Following my own work,
[Gligor, Donescu; April 2001] updated their
modes to use a single key and
to deal with messages of arbitrary bit length.
What is this attack described by Ferguson?
A 2002 note by Niels Ferguson,
Collision attacks on OCB,
points out that, after about 264 blocks of messages are queried
(300 million terabytes), all authenticity with OCB is forfeit.
This is just the usual birthday attack.
Ferguson finds this alarming.
He should not.
Security of almost every encryption (or authentication) scheme based
on a 128-bit blockcipher
vanishes at a rate of σ2/2128 where
σ is the number of blocks queried.
And security, once lost, is routinely “completely” lost—what
Ferguson seems to object to most.
There are a few blockcipher-based AE schemes that have been designed to achieve
security beyond the birthday bound;
for example, see
Authenticated
Encryption Mode for Beyond The Birthday Bound Security, by T. Iwata.
My own belief is that, for a standardized mode of operation based on a 128-bit blockcipher,
beyond-birthday-bound security is good to have only it is achieved
easily and cheaply.
Birthday-bound attacks (as well as good cryptographic hygine)
motivate rekeying well in advance of birthday-bound concerns.
In RFC 7253 we say
that a given key should be used to encrypt at most 248 blocks (about 280 terabytes).
What is a nonce and why do you need one?
In OCB, you must present a nonce each time you want to
encrypt a string.
When you decrypt, you need to present the same nonce.
The nonce doesn’t have to be random or secret or unpredictable.
It does have to be something new with each message you encrypt.
A counter value will work for a nonce, and that is what is recommended.
It doesn’t matter what the counter is initialized to.
In general, a nonce is a string that is used used at most one time
(either for sure, or almost for sure) within
some established context.
In OCB, this “context” is the “session” associated to the
underlying encryption key K.
For example, you may distribute the key K by a session-key
distribution protocol, and then start using it.
The nonces should now be unique within that session.
Generating new nonces is the user’s responsibility, as
is communicating them to the party that will decrypt.
A nonce is nothing new or strange for an encryption mode.
If there were no nonce there would be only one
ciphertext for each plaintext, key, and AD, and this means that the
scheme would necessarily
leak information (e.g., is the plaintext for
the message just received the same as the plaintext for the
previous message received?).
In CBC mode the counterpart of a nonce is called an IV (initialization vector)
and it needs to be adversarially unpredictable if you’re going to meet a
strong definition of security.
In OCB we have a weaker requirement on the nonce, and
so we refrain from calling it an IV.
What happens if you repeat the nonce?
You’re going to mess up authenticity for all future messages, and you’re
going to mess up privacy for the messages that use the repeated
nonce.
So don’t do this.
It is the user’s obligation to ensure that nonces don’t
repeat within a session.
In settings where this is infeasible, OCB should not be used.
We note that most conventional encryption modes fail, often quite miserably,
if you repeat their supplied IV/nonce.
Only recently (2006) did cryptographer’s develop a notion for an encryption
scheme being maximally “resilient” to nonce-reuse.
The notion is due to Tom Shrimpton and me and we also developed a scheme,
SIV, to solve this problem. But it’s a conventional
composed scheme: half the speed, or worse, of OCB.
SIV makes a nice alternative to a composed scheme like CCM,
EAX, offering comparable performance but a better
security guarantee.
Is there code available? Is it free?
Yes there’s code and yes it’s free.
Ted Krovetz wrote some nice code.
See the top-level OCB page for a link.
Other code for OCB is showing up in various cryptographic libraries.
For example, OCB is now in OpenSSL
In correctly coding OCB, I think the biggest difficulty is
endian problems. The spec is subtly big-endian
in character, a consequence of it’s use of “standard”
mathematical conventions.
If your implementation doesn’t agree with the reference one,
chances are there’s some silly endian-related error.
There are well-known perils with implementing encryption algorithms,
such as needlessly opening the door to
timing attacks.
Are OCB test vectors available?
OCB test vectors can be found near the end of
RFC 7253.
Is it safe to use a new algorithm in a product / standard?
In the past, one had to wait years
before using a new cryptographic scheme;
one needed to give cryptanalysts
a fair chance to attack the thing. Assurance in a scheme’s correctness
sprang from the absence of damaging attacks by smart people,
so you needed to wait long enough that at least a few smart people would try,
and fail, to find a damaging attack.
But this entire approach has become largely outmoded,
for schemes that are not true primitives,
by the advent of provable security.
With a provably-secure scheme assurance does not stem from a failure
to find attacks; it comes from proofs,
with their associated bounds and definitions.
Our work includes a proof that OCB-E
is secure as long as blockcipher E is secure (where E is an arbitrary block
cipher and “secure” for OCB-E and secure for E
are well-defined notions).
Of course it is conceivable that OCB-AES could fail because AES
has some huge, unknown problem.
But other issues aren’t really of concern.
Here we’re in a domain
where the underlying definition is simple and rock solid;
where there are no “random oracles” to worry about;
and where the underlying cryptographic assumptions are completely standard.
Are there competing integrated authenticated-encryption proposals?
There are, although none are as refined as OCB.
See the Krovetz-Rogaway paper
The software performance of authenticated-encryption modes
for a chart pointing to a number of AE schemes. Going back to the original
integrated (aka, one-pass) schemes from Jutla and
from Gligor-Donescu:
- Jutla (2000) propose two modes, IACBC and IAPM.
The latter is the parallelizable scheme and is therefore the one to compare to OCB.
Various methods are specified for offset
generation in IAPM, but none are competitive with OCB.
Jutla assumes that messages have a multiple of n bits; padding is used,
presumably, to deal with other lengths.
Once a padding regime is added, say obligatory 10*-padding,
the length of ciphertexts will
be longer than OCB ciphertexts any time that the
message being encrypted is
a non-multiple of 16 bytes.
IAPM uses twice the key material of OCB.
Associated data is not handled.
- Gligor and Donescu (2000) propose
four authenticated-encryption schemes, which the authors call
XCBC$-XOR, XCBC-XOR, XCBCS-XOR, and XECBS-XOR.
Only the last of these modes
is parallelizable.
The addition of a parallelizable scheme
came subsequent to the publication of Jutla’s work,
and XECBS-XOR is similar to Jutla’s IAPM.
XECBS-XOR uses mod 2n addition instead of mod-p addition.
This difference might suggest an efficiency
improvement, but this is unclear, as
[Jutla] uses one mod-p addition and three 128-bit xors while
[Gligor, Donescu] uses three 128-bit additions and one 128-bit xor.
One expects the use of an additive ring (integers mod 2n) instead of
a field (GF(p) or GF(2n)) to worsen any possible security bound by
at least a log factor.
No proof has been given for this mode.
Following my own work, [Gligor, Donescu] includes techniques
so as to use a single key and to deal with messages of
arbitrary bit length. But the techniques are not pushed
as far as with OCB and there is ciphertext-expansion
for all messages which are a non-multiple of the 16 bytes.
In my opinion, there remains no desirable, standardized, integrated-scheme alternative
to OCB; no other integrated scheme has as yet gotten
any traction in products or standards.
But various composed schemes are reasonable alternatives to OCB,
particularly CCM and GCM.
And the CAESAR competition,
which has drawn an amazing 57 submissions, is likely to eventually
yield some well-vetted alternatives.
Are there competing composed
authenticated-encryption proposals?
The traditional approach for achieving authenticated-encryption was to use
generic composition.
Using separate keys, you should encrypt the plaintext and then MAC the
resulting ciphertext. You can use any encryption scheme and any MAC
that you like, and the composite scheme is guaranteed to do what it should do.
To offer the same basic “service” as OCB
you’ll need, in the end, to do something like this. For privacy,
use CBC mode with ciphertext-stealing and an IV derived by enciphering
the nonce. For authenticity,
use the CBC MAC variant known as CMAC.
Use standard key separation to make all the needed keys.
Make sure the MAC is taken over the IV of the encryption scheme.
There are various pitfalls people run into when trying to do a homebrewed
combination of privacy and authenticity. Common errors include:
(1) a failure to properly perform key separation;
(2) a failure to use a MAC that is secure across different message lengths;
(3) omitting the IV from what is MACed;
(4) encrypting the MACed plaintext as opposed to the superior method
(at least with respect to general assumptions)
of MACing the computed ciphertext.
For all of these, I cannot advise people to roll-their-own
authenticated-encryption scheme.
Even standards get things wrong.
A Eurocrypt 2014
paper by Namprempre, Shrimpton, and me reexamines the generic-composition approach and what
has been understood of it.
It turns out that even standards (like the ISO standard mentioned above) do not get things rights.
The problem, in part, is that the theory literature’s early starting points and constructive goals
do not match up with standardized starting points and the conventional AEAD goal.
To date, the most significant composed authenticated encryptions
schemes are
CCM and GCM.
Some other techniques include
SIV and
EAX.
All of these modes comprise IP-free means of performing authenticated-encryption with associated-data.
-
CCM is an authenticated-encryption mode designed by
Housley, Ferguson, and Whiting. It’s inspired by the generic
composition of counter mode encryption and the CBC MAC
(but CCM is not in fact an instance of generic composition).
CCM was developed as a less-efficient but IP-free alternative to OCB.
It is specified in
NIST Special Publication 800-38C.
It’s kind of a cobbled-up thing,
but the it got into 802.11i,
and then other standards. The bounds are good and no significant weaknesses are
known.
Most criticisms focus on efficiency concerns, including
the one I wrote with David Wagner, A Critique of CCM.
-
GCM is an authenticated-encryption mode designed by
McGrew and Viega.
It combines a privacy-only encryption mechanism (CTR mode)
with a Carter-Wegman MAC,
the latter based on multiplication in the finite field with 2128 points.
The initial purpose of GCM was to have a parallelizable, hardware-efficient, and
patent-free AEAD scheme.
Being parallelizable means that it is useful for
high-speed hardware-based applications.
Having to implement multiplies in GF(2128) can
be slow unless large tables are used, but it’s pretty fast
if you use such tables, and hardware chip area for GF(2128)
multiplication can be low.
New Intel chips support a “carryless multiply” instruction meant to
help the mode run fast.
GCM is specified in Draft NIST publication 800-38D.
We also elaborate on SIV, a deterministic or misuse-resistant authenticated-encryption
mode. It was designed by
Rogaway and Shrimpton to solve the “key wrap” problem.
When used as a nonce-based AEAD scheme, SIV has the unusual property that
it doesn’t “break” if a nonce should get reused: all that
happens is that repetitions of this exact (nonce, AD, plaintext)
are revealed.
The mode can also be used without any nonce and, when used as such,
all it reveals are repetitions in (nonce, AD, plaintext) pairs.
SIV suffers from a latency problem (unavoidable for the
deterministic or misuse-resistant AEAD goal): one must not only
make two passes over the input, but one cannot output any ciphertext
bits until all plaintexts bits are read.
SIV is described in a
Eurocrypt 2006 paper and an associated spec,
RFC 5297, by Dan Harkins.
The main advantage of OCB over CCM, GCM, and other composed schemes is software
speed. See the performance page
for data.
Is OCB patented?
It was; I had patents
7,046,802,
7,200,227,
7,949,129, and
8,321,675.
But I intentionally allowed all of my patents to lapse.
I placed all OCB-related IP that I owned in the public domain.
You don’t need to get any sort of permission from me, or pay me anything, to use OCB.
There were further patents in the AE space, including those of
Jutla (IBM)— 6,963,976,
7,093,126, and
8,107,620—and of
Gligor and Donescu (VDG)—6,973,187.
I have never known if the claims of these patents read against OCB.
It is difficult to answer such a question, and I was never in a position to say.
Hopefully all authenticated-encryption IP is invalid,
has expired by now, or was never relevant to using OCB.
Do I need a license?
No. See the question above.
Who is the author of this webpage?
I am,
Phillip Rogaway,
a professor in the
Department of Computer Science at the
University of California, Davis.
I have also been a regular visitor to universities in Thailand,
most often at the Department of Computer Science at
Chiang Mai University.
For 20 years I’ve worked to develop and popularize
a style of cryptography I call practice-oriented provable security.
This framework is a perfect fit
to the problem of designing an authenticated-encryption scheme.
One of the “outputs” of practice-oriented provable security
has been cryptographic schemes that are well-suited standards.
In particular, I am co-inventor on the schemes
known as CMAC, DHIES, EAX, OAEP, PSS, and XTS,
which are in standards from ANSI, IEEE, ISO, and NIST.
The kind of academic work I do can be seen by looking at
dblp
or
google Scholar.
Back to the
OCB homepage
|