ECS 170: Introduction to AI
Instructor: Rao Vemuri
Homework Assignment # 1 (Submit in
hard copy format)
Due: 21 January 2003
(100 points)
This problem is based on Problem Formulation
1. (20 points). The Cannibals-Missionaries Problem. Consider the problem of three cannibals and three edible missionaries seeking to cross a river in a boat that can hold at most two individuals and can be navigated by one or any combination of two individuals. Under no circumstances can the missionaries be outnumbered by the cannibals, anywhere.
This problem has been solved in a
variety of ways. For our problem, let the ordered pair (m, c) denote the number
of cannibals and missionaries on the first bank.
(a) Give your version of a solution to this problem by writing a sequence of
state transitions. Use the above cited ordered pair as the state and an arrow
to indicate a state transition.
(b) This problem is simple to solve once you have the correct representation.
One way of doing this is to represent the
states as discrete points in a two-dimensional m-c plane. Using m as the
abscissa and c as the ordinate, plot ALL the possible states. All these states
are NOT admissible; i. e. , some states are prohibited by the rules of the
problem. Identify the admissible states by solid circles (i. e., dots completely
filled) and inadmissible states by open circles.
(c) Now show on this diagram, every boat passage by a directed arrow. That is,
a transition, such as (3,3) --> (3,1) will be represented by a directed
arrow from (3,3) to (3,1). Show the complete solution by a sequence of directed
arrows.
These problems are based on Search
Consider a road map such as the one shown in Figure (Ignore the arrows on the edges. They are not supposed to
be there)
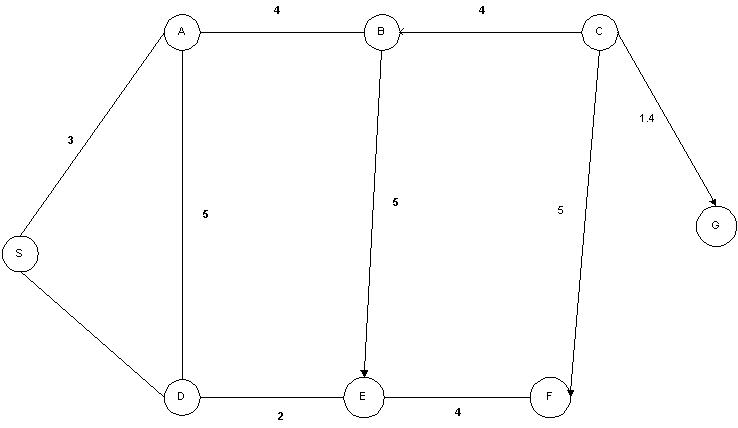
2. (10 points) Draw a tree of all loop-free paths that is equivalent to the net shown above. When a node has more than one child, arrange them in alphabetical order.
2. (10 points) Show how DFS would search the net shown in the above figure
3. (10 points) Show how BFS would search the net shown in the above figure
4. (10 points) On page76 of the book, the authors said that they would not consider the case of negative path costs. Suppose that a negative lower bound c is placed on the cost of any given step (that is, negative costs are allowed, but they cannot go below a specified c). Does this allow uniform-cost search to avoid searching the whole tree? Explain in one or two sentences.
5. (20 points) The GENERAL-SEARCH algorithm executes the following three
steps in the indicated order: goal test, generate, ordering function. It is a
shame to generate a node that is in fact a solution, but fail to recognize it
immediately because the ordering function fails to place it first in the queue.
(a) Write a version of GENERAL-SEARCH that tests each node as soon as it is
generated and stops immediately if it has found the goal.
(b) Show how GENERAL-SEARCH can be used unchanged to do this by giving it the proper
ordering function.
6 (10 points) Suppose that we run a greedy algorithm with h (n) = - g(n). What sort of search does this greedy search emulate? Explain.
7. (10 points) Prove that IF the heuristic function h obeys the
triangle inequality, THEN the f-cost along any path in the search tree is
non-decreasing. (The triangle inequality says that the search cost from A to B
and B to C must not be less than the cost from A to C directly.)
Department of Computer Science
University of California at Davis
Davis, CA 95616-8562
Page last modified on 1/15/2003